Sure, Heres A Blog Post Title In Traditional Chinese Using Your Keyword At The Beginning:《球壳转动惯量:探索运动中的物理现象》
转动惯量 Part 1
用戶搜尋的關鍵字: 球 壳 转动 惯量 圆环的转动惯量, 转动惯量推导, 转动惯量和力矩, 常见转动惯量, 转动惯量计算公式, 转动 惯量 公式 表, 圆柱体转动惯量, 角动量和转动惯量
球壳转动惯量:深入解析与实际应用
什么是转动惯量?
在物理学中,转动惯量是描述物体在旋转运动中对抗改变自身旋转状态的性质。对于球壳转动惯量而言,这一概念变得更加有趣而复杂。本文将深入探讨球壳转动惯量的各个方面,包括其定义、计算方法、影响因素以及实际应用。
描述转动惯量的概念
转动惯量,也称为惯性矩,是一个物体旋转时惯性的度量。它描述了物体在旋转运动中对于改变自身状态的抵抗程度。在球壳的背景下,转动惯量是指球壳绕其直径轴线旋转时所具有的惯性。
为了更好地理解转动惯量的概念,可以将其与物体的质量概念进行对比。质量是物体对于改变其运动状态的抵抗程度,而转动惯量则是物体对于改变其旋转状态的抵抗程度。在球壳的例子中,转动惯量可以帮助我们理解球壳在旋转运动中的稳定性和惯性。
球壳的形状与转动惯量
球壳的形状对其转动惯量有着重要的影响。不同半径、密度分布等因素都会改变球壳的转动惯量。在这一部分,我们将讨论球壳的形状如何影响其转动惯量,并通过具体案例进行说明。
球壳的半径与转动惯量
球壳的半径是影响其转动惯量的关键因素之一。根据转动惯量的定义,半径越大,物体对于绕轴旋转的抵抗程度越大。这是因为较大的半径意味着更多的质量分布在离轴较远的位置,增加了旋转的惯性。
密度分布与转动惯量
球壳的密度分布同样影响着其转动惯量。如果球壳的质量分布不均匀,即某些区域的质量较大,而其他区域较小,那么其转动惯量将会受到影响。这种不均匀的密度分布会导致轴线附近的质量分布不同,从而改变了整个球壳的旋转性能。
球壳转动惯量的计算公式
了解如何计算球壳的转动惯量对于深入理解这一概念至关重要。下面是计算球壳转动惯量的数学公式及其解释:
I=32mr2
其中,I 为球壳的转动惯量,m 为球壳的质量,r 为球壳的半径。
这个公式表明,球壳的转动惯量与其质量和半径的平方成正比,符合我们之前在形状影响中讨论的概念。
球壳转动惯量的物理解释
转动惯量背后有着深刻的物理原理。质量分布、转动轴的位置等因素都会对转动惯量产生影响。在这一部分,我们将深入解释这些物理原理,帮助读者更好地理解球壳转动惯量的形成过程。
质量分布的影响
球壳的质量分布是影响其转动惯量的重要因素。当质量分布越均匀时,转动惯量越容易计算。然而,如果质量分布不均匀,需要进行积分或其他复杂的数学运算来准确计算转动惯量。
转动轴的位置
转动轴的选择也会对转动惯量产生影响。通常情况下,选择与质量分布对称的轴会使计算更加简单。不同的轴位置会导致不同的转动惯量,因此在实际问题中正确选择转动轴至关重要。
球壳转动惯量的应用
转动惯量不仅仅是一个理论概念,它在实际生活中有着广泛的应用。在这一部分,我们将探讨转动惯量在工程、机械设计以及物体运动方面的具体应用案例。
工程中的应用
在工程领域,特别是涉及到旋转部件的设计时,了解转动惯量是至关重要的。例如,在设计飞机的旋转部件或者机械装置时,工程师需要确保其转动惯量在合理范围内,以保证系统的稳定性和性能。
机械设计中的应用
机械设计过程中,转动惯量是设计师考虑的重要因素之一。通过调整零件的形状、密度分布等参数,设计师可以优化机械系统的转动性能。这种优化可以提高机械系统的效率,减少能源浪费。
物体运动方面的应用
在研究物体的运动时,特别是围绕轴线旋转的运动,转动惯量是分析物体运动的关键参数之一。例如,在研究地球自转时,了解地球的转动惯量可以帮助科学家更好地理解地球自转的稳定性和变化。
球壳转动惯量与动能
转动惯量与动能之间存在着密切的关系。在这一部分,我们将分析转动惯量如何与动能相关联,并讨论它们之间的数学关系和物理意义。
动能与转动惯量的数学关系
动能(K)与转动惯量(I)之间的数学关系可以通过以下公式表示:
K=21Iω2
其中,K 为动能,I 为转动惯量,ω 为角速度。
这个公式表明,动能与转动惯量成正比,而角速度的平方成正比。这反映了转动惯量对于物体旋转运动的稳定性的影响。
物理意义
从物理角度来看,转动惯量与动能之间的关系表明了物体在旋转运动中具有的能量。较大的转动惯量意味着物体在相同角速度下具有更大的动能,反之亦然。这对于设计旋转系统时的能量管理和效率提升至关重要。
不同材料对球壳转动惯量的影响
材料的密度、强度等特性对球壳转动惯量有着直接的影响。在这一部分,我们将研究不同材料对球壳转动惯量的影响,并讨论材料选择对于优化转动性能的重要性。
密度对转动惯量的影响
不同材料的密度差异会导致相同质量的球壳具有不同的体积。由于转动惯量与质量和半径的平方成正比,因此密度的变化直接影响着转动惯量的大小。在工程中,通过选择合适的材料密度,可以调整球壳的转动性能。
强度对转动惯量的影响
材料的强度也会对球壳的转动惯量产生影响。强度较高的材料在相同质量下可能具有较小的体积,从而影响球壳的转动惯量。在一些特殊的应用场景中,需要考虑强度对转动性能的影响,以确保系统的稳定性和安全性。
实验方法与测量转动惯量
了解如何测量球壳的转动惯量对于验证理论计算结果和实际应用至关重要。在这一部分,我们将介绍测量球壳转动惯量的实验方法,包括旋转实验、数学模型和实验装置等方面的详细说明。
旋转实验
通过设计旋转实验,可以直接测量球壳在旋转过程中所具有的转动惯量。这通常涉及将球壳固定在旋转轴上,并测量所需的旋转力矩以及相应的角加速度。通过观察实验结果,可以验证理论计算的准确性。
数学模型
建立数学模型是测量转动惯量的另一种方法。通过观察实际运动,并将其建模为数学方程,可以推导出与转动惯量相关的物理参数。这种方法通常需要一定的数学和物理知识,但可以提供准确的实验结果。
实验装置
选择合适的实验装置对于测量转动惯量也至关重要。合理设计的实验装置可以减小误差,提高实验的可靠性。通常情况下,实验装置应当考虑到球壳的形状、大小以及测量精度的要求。
球壳转动惯量的变化与运动状态
球壳在不同运动状态下其转动惯量会发生变化。在这一部分,我们将探讨球壳在匀速转动、加速转动或停止状态下转动惯量的差异,并解释这些变化背后的物理原理。
匀速转动状态下的转动惯量
在匀速转动状态下,球壳的转动惯量保持不变。这是因为匀速旋转意味着角速度恒定,根据转动惯量的定义,它与角速度的平方成正比。因此,在匀速转动状态下,球壳的转动惯量保持稳定。
加速转动状态下的转动惯量
在加速转动状态下,球壳的转动惯量会发生变化。加速度引起了角速度的变化,从而影响了转动惯量。在这种情况下,需要考虑加速度对于转动惯量的贡献,以更准确
類別: 統計 59 球 壳 转动 惯量

如何求转动惯量?
在經典力學中,轉動慣量(又稱質量慣性矩,簡稱慣矩)是一個重要的物理量,常以I或J表示,其國際單位為kg·m2。轉動慣量描述了物體對於繞某一軸旋轉的難易程度,即物體的轉動慣性。對於單一質點而言,轉動慣量的計算公式為I = mr2,其中m為質點的質量,r為質點與轉軸的垂直距離。這個公式表明了質量越大或質點離轉軸越遠,轉動慣量就越大,反映了物體對於旋轉的慣性。理解轉動慣量對於分析物體的旋轉行為和解決相關問題至關重要。
力矩是什么意思?
什麼是力矩?力矩是描述力對物體產生轉動效應的物理量。力矩的大小由力和力臂的乘積來表示,這稱為力對轉動軸的力矩。換句話說,某一點的力矩大小取決於該點到力的作用線所引垂直線的長度(即力臂)乘以力的大小。力矩的方向則是由力矩的右手螺旋法則來確定,即該方向垂直於垂直線和力所構成的平面。藉由這樣的描述,讀者更容易理解力矩是如何衡量力對物體轉動效應的。
角速度的单位是什么?
什麼是角速度的單位?在物理學中,角速度是描述物體圍繞著一個固定點旋轉的速度。它的單位通常使用弧度每秒(rad/s)來表示。弧度是一個角度的測量單位,而角速度則指的是物體每秒在這個角度上轉過的弧度數。這個單位提供了一種量度物體在一段時間內旋轉的方式,使我們能更好地理解和比較不同物體的旋轉速度。所以,如果你想了解一個物體圍繞點旋轉的速度,角速度的單位就是弧度每秒。
詳細 30 球 壳 转动 惯量




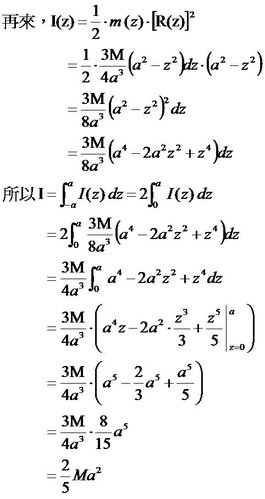




在這裡查看更多內容: taomalumdongtien.net
了解有關該主題的更多信息 球 壳 转动 惯量.